分层知识结构中的个人优化间隔重复

原文：Optimized, Individualized Spaced Repetition in Hierarchical Knowledge Structures - Justin Skycak

作者：Justin Skycak 发表于 2023 年 10 月 5 日

在像数学这样有层级的知识体系中应用间隔重复是复杂的，这主要是因为高阶主题的复习会对低阶主题产生「涓滴效应」，从而使得这些主题相关的复习排期也需要改变，当然这些重复可能过早，不能算作一次完整的复习，因此需要适当地折算其效果。为了应对这一挑战，我开发了一个名为部分隐式重复 (Fractional Implicit Repetition, FIRe) 的模型。这个模型不仅考虑了隐式的「涓滴」复习，还通过巧妙选择复习内容，让某个主题的隐式复习能连带完成其他待复习主题（就像多米诺骨牌那样），从而显著减少了所需的总复习次数。更为关键的是，该模型能够根据每个学习者在不同主题上的表现，动态调整间隔重复的节奏，在学习者能力和主题难度这两个相互制约的因素之间找到最佳平衡点。

据我所知，当前关于确定最佳复习间隔的数学模型研究，仅限于独立的类似抽认卡的学习任务场景。然而，许多学科实际上是由高度关联的「问题解决」知识构成的复杂体系。

那么，在这种高度关联的问题解决知识体系中，我们该如何有效利用间隔效应（即进行间隔重复）？乍一看，这似乎只需对传统的 Anki 抽认卡系统做一些简单调整即可：

• 一方面，我们可以轻松地将传统的记忆型抽认卡升级为解题练习：不再在每张卡片上使用固定的问题和答案，而是只标注主题名称，然后从该主题的问题库中随机抽取一个问题。如果你能正确解答这个随机问题，就视为「成功回忆了卡片内容」。

• 在这个过程中兼顾知识点的先后顺序也很简单：只有在成功掌握了所有前置知识后，才能引入新的主题。（在将新主题正式纳入间隔重复牌组之前，你还需要完成一个专门的学习单元。在这个单元中，你将在充分的指导和支持下，主动学习并展示你对新问题解决技巧的理解和应用能力。）

然而，魔鬼藏在细节里，尤其是在更新重复规划时，层级结构带来了显著的模型复杂性：例如，对于高级主题的重复应该「涓滴」，以更新那些被隐式练习到的基础主题的重复规划（同时要适当折扣，因为这些复习通常发生得过早，在效果上不能完全算作下一次正式复习）。

为了克服这个障碍，我在 Math Academy 开发了一个部分隐式重复 (Fractional Implicit Repetition, FIRe) 模型。这个模型不仅考虑了隐式的「涓滴」重复，而且还

• 通过巧妙选择复习内容（包括新课程），使其隐式的重复能像多米诺骨牌效应一样连锁「触发」其他待复习内容，从而最大限度地减少所需的复习次数，并且

• 针对每位学生在每个具体主题上的学习情况，对间隔重复过程进行个性化调整。这一过程需要权衡学生能力和主题难度这两个相互制约的因素——学生能力越强，整体学习进度越快；而主题难度越高，学习速度则相应放缓。

这个模型是在 2019 年至 2022 年间经过深入研究与开发而成的成果。尽管具体的实施细节属于专有技术，但我可以在这里分享一些核心理念。目前，该模型的基本组件已经相当稳定（尽管我每年仍在持续改进）。

重复压缩

一个对间隔重复的常见批评是它需要的复习量太大了。这种批评在使用间隔重复学习互不相关的抽认卡时可能成立，但在数学学习中，我们可以利用数学学科的特殊性来规避这个问题。

与孤立的抽认卡不同，数学是一个层次分明、高度关联的知识体系。当学生解决一个高级数学问题时，他们实际上在潜移默化中练习了许多基础数学技能。换言之，在数学领域中，高级技能往往包含了众多基础技能。

因此，当学生需要进行复习时，这些复习任务通常可以被压缩成一个规模更小的学习任务集。这个精简的任务集能够隐式包含（即重复练习）所有待复习的内容。我将这个过程称为重复压缩（repetition compression）。

为了更好地阐述这个概念，让我们看一个具体的乘法例子，即将两位数 39 乘以一位数 6：

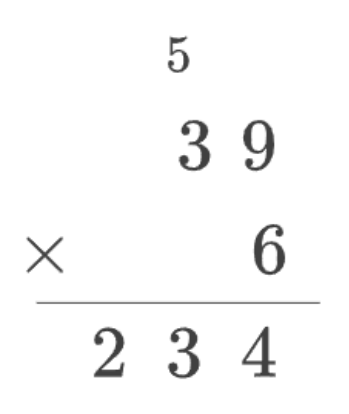
要完成上述乘法运算，我们必须对一位数字进行乘法运算，并将一位数字加到两位数字之上：

• 首先，计算 6 × 9 = 54。我们将 5 进位，在结果的个位写下 4。

• 然后，计算 6 × 3 = 18，再加上进位的 5，得到 18 + 5 = 23。我们将 23 写在结果的十位和百位。

换句话说，「两位数乘以一位数」这个运算实际上包含了「一位数乘法」和「一位数与两位数的加法」这两个基本运算。

我们可以通过下面的包含图来可视化这种关系。包含图与前置知识图类似，但有一个重要区别：这里的箭头表示一个较简单的主题被一个更高级的主题所包含。（需要注意的是，被包含的主题通常是前置知识，但并非所有前置知识都会被完全包含。）

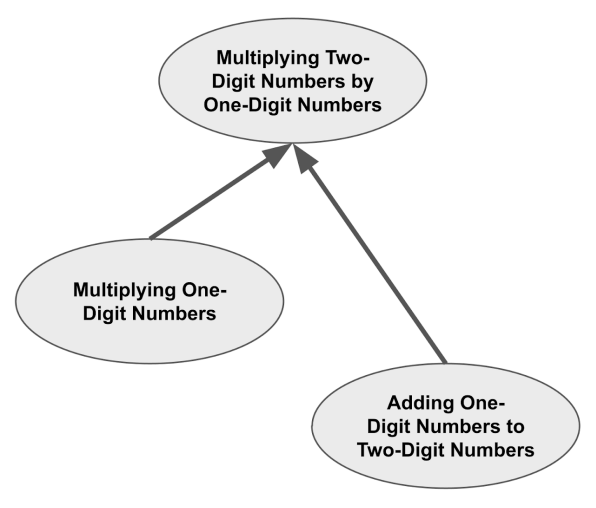
现在，假设一个学生需要复习这三个主题。由于知识间存在包含关系，他们实际上只需要复习「两位数乘以一位数」这一主题。当完成这个复习时，学生也在练习了这些技能，从而隐式重复了其包含的主题。

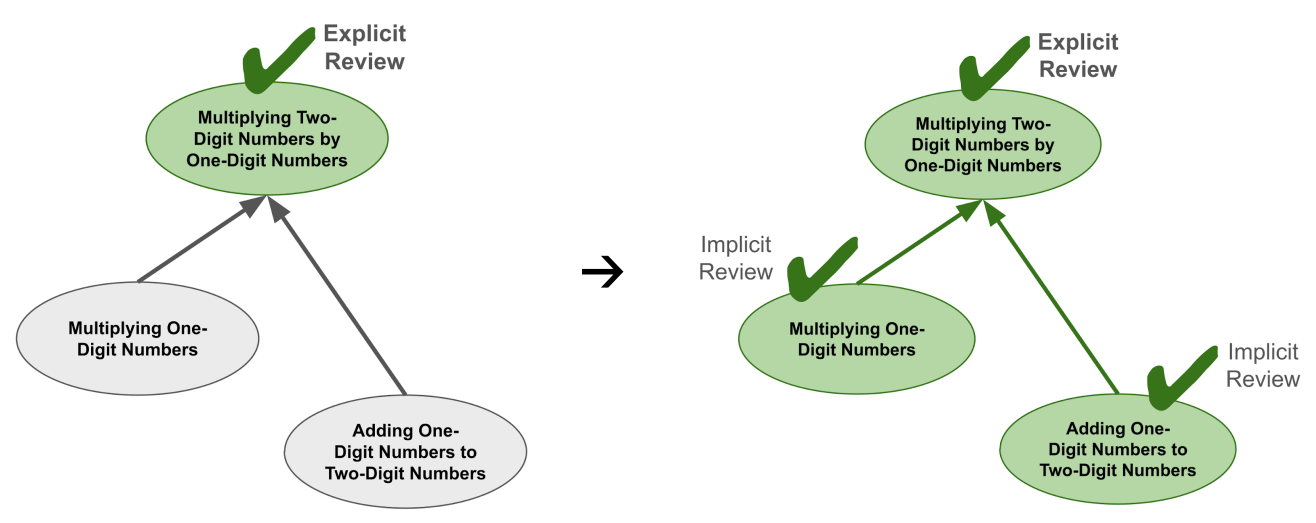
总的来说，知识之间的包含关系越多，实际需要的复习就越少。而数学恰恰是一个存在大量包含关系的学科！

学习效率

在物理学中，光速是一个不可逾越的界限。它代表了任何物质能够达到的理论最高速度，是一个宇宙常数。

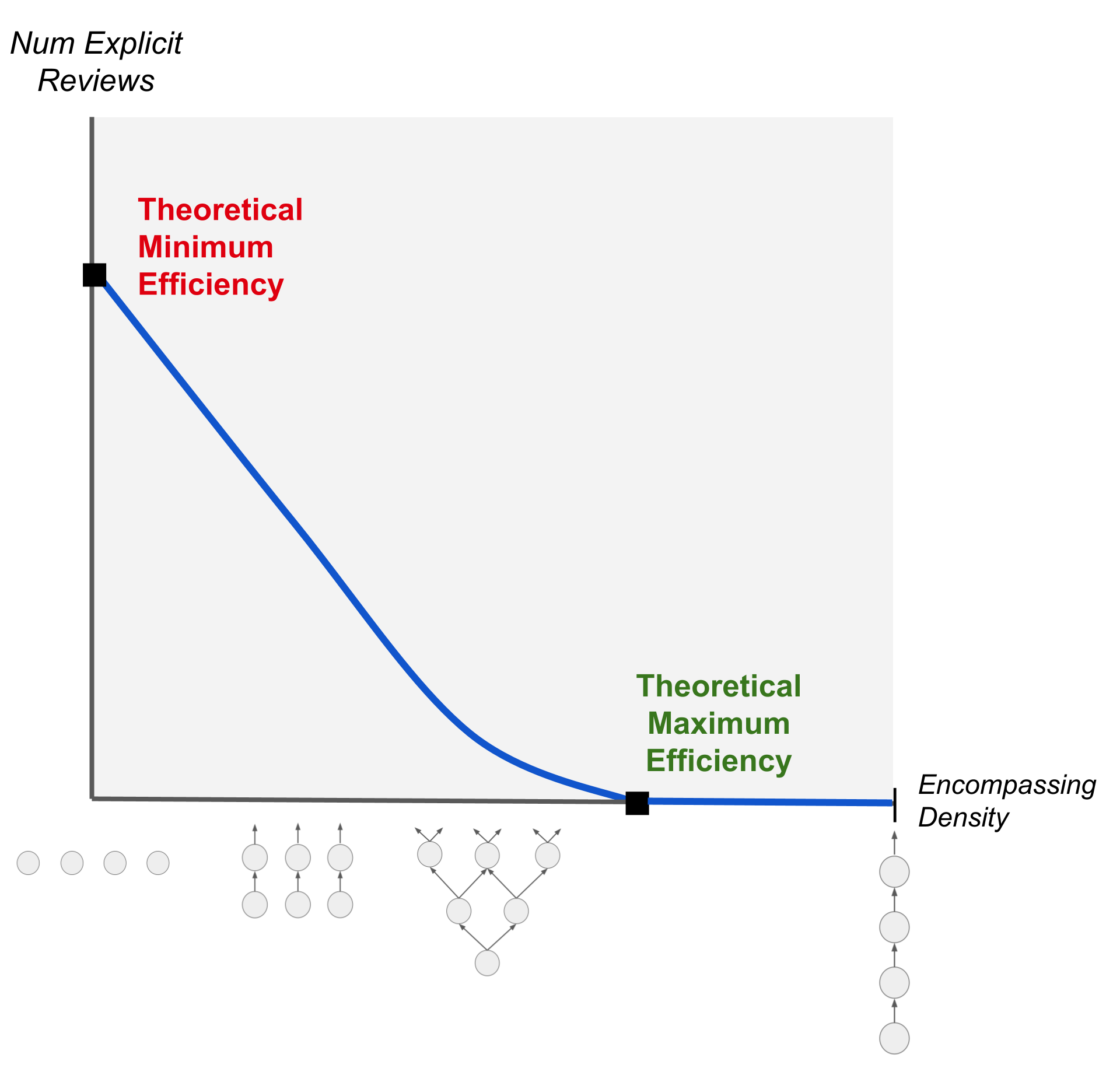
在间隔重复的领域中，我们也有一个类似的概念：理论最大学习效率。从理论上讲，如果我们拥有一个结构良好、内容紧密关联的知识体系，我们就有可能无需刻意回顾之前学过的内容，就完成所有的间隔重复。

为了更直观地理解这一点，我们可以想象一系列逐层包含的主题：第一个主题完全包含在第二个之中，第二个又完全包含在第三个之中，第三个进一步包含在第四个之中，以此类推。

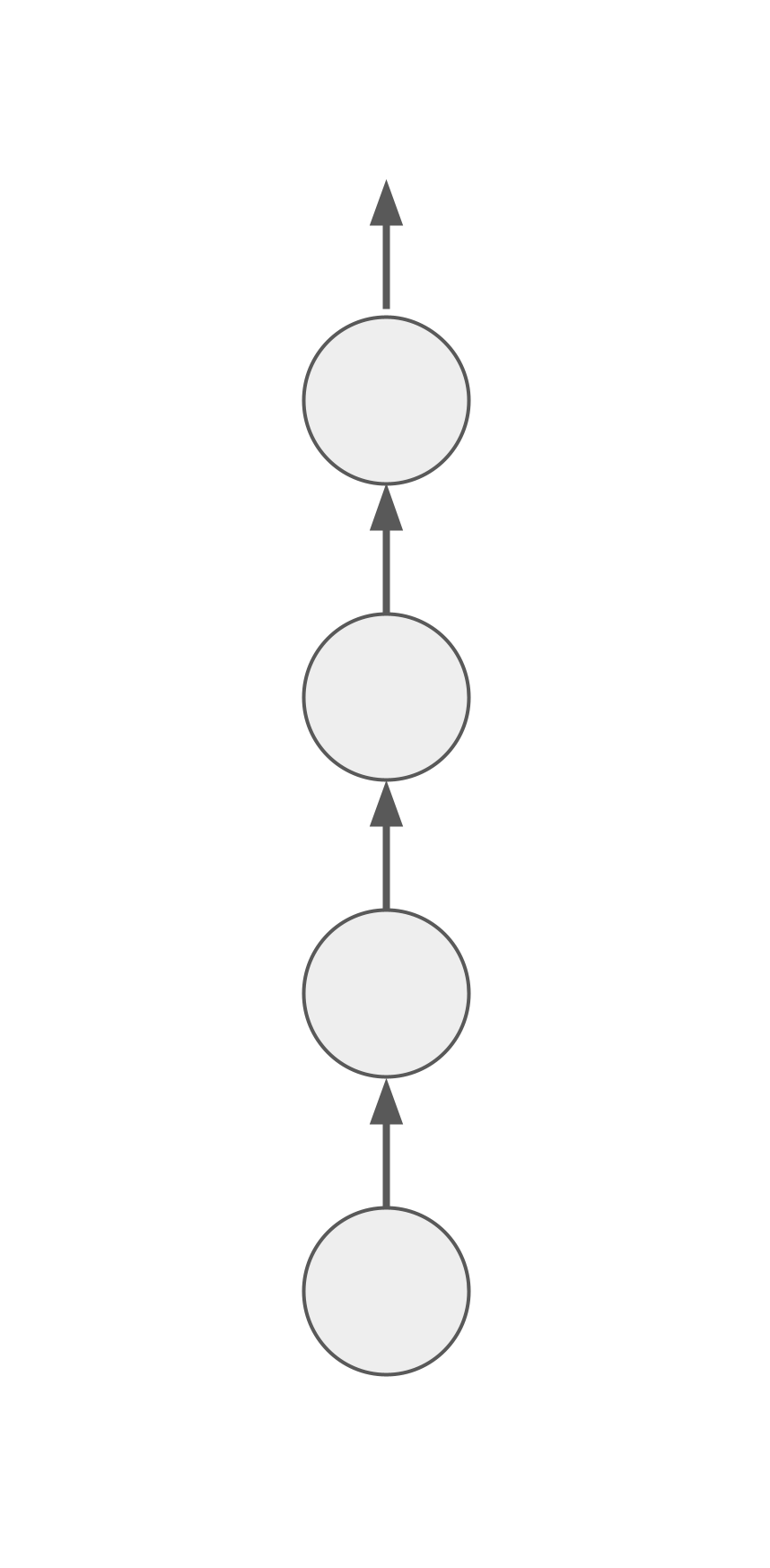
每当你学习一个新主题时，所有相关的下级主题都会得到隐式重复。理想情况下，如果你总能找到新的主题来学习，唯一需要进行显式重复的情况就是当你反复尝试却无法掌握某个新主题时。

与此相对的是理论最小学习效率的概念。这种情况等同于使用独立的抽认卡，或者说是一组没有任何内在联系的知识点。

在这种情况下，任何知识点都无法从其他知识点获得隐式重复。每次复习都必须显式进行。

值得注意的是，「知识结构图并不需要完全或几乎完全地相互包含，就能使其最大学习效率接近理论极限」。即使大多数知识点之间没有包含关系，少量的包含关系也能显著提高整体学习效率。

部分隐式重复（FIRe）

在介绍了重复压缩的概念后，让我们进一步探讨通过包含图实现部分隐式重复 (fractional implicit repetitions, FIRe)。

FIRe 将传统的间隔重复扩展到具有层级结构的知识体系中，在这种体系中：

1. 高级主题的重复练习会通过知识间的包含关系，隐式「涓滴」到相关的基础主题，并且

2. 频繁获得隐式重复的基础主题会适当降低这些重复的权重（因为它们通常发生得过早，在效果上不能完全算作下一次正式重复）。

具体实例

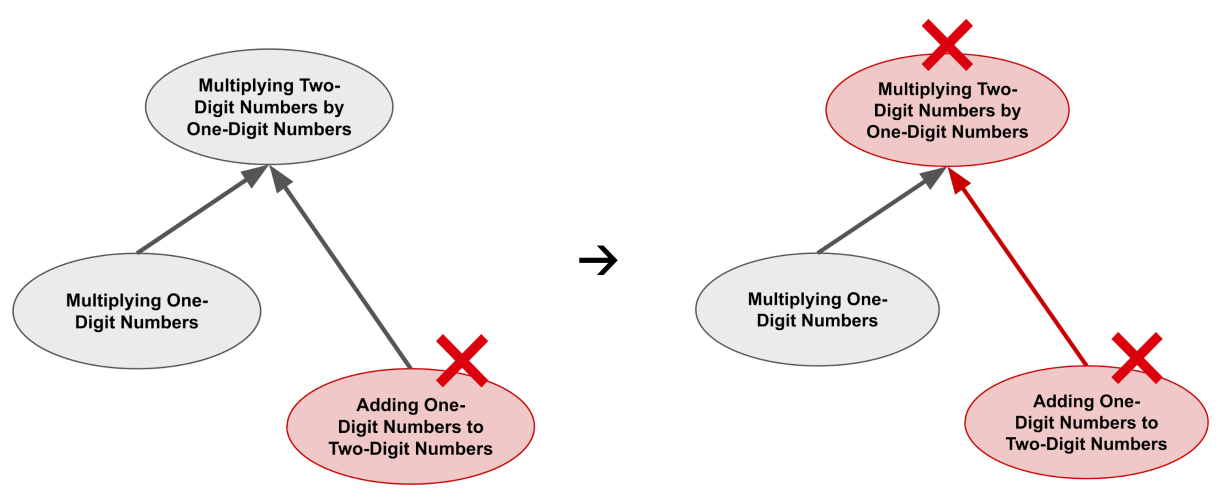
让我们用一个具体例子来阐述这个概念。请回想一下，「两位数乘一位数」这个技能实际上包含了「一位数相乘」和「一位数加两位数」这两个基础技能。

假设你成功通过了「两位数乘一位数」的重复练习，这次成功的练习不仅仅惠及这个特定技能，它还会「反哺」到「一位数相乘」和「一位数加两位数」这两个基础技能。这是因为你刚刚证明了你仍然熟练掌握这些基础技能。

相反，如果你在「一位数加两位数」的重复练习中失败了，这次失败不仅影响这个特定技能，还会「连带影响」到「两位数乘一位数」这个更复杂的技能。毕竟，如果你连一位数加两位数都做不到，你就更不可能完成两位数乘一位数的计算了。同理，如果你在「一位数相乘」的重复练习中失败，也会产生类似的连锁反应。

重复流的可视化

请注意，重复流（repetition flows）可以延伸很多层——不仅仅是直接包含的主题，还有被包含主题所包含的「二阶」主题，然后是被二阶主题包含的三阶主题，以此类推。

在视觉上，得分像闪电一样向下流经知识图。

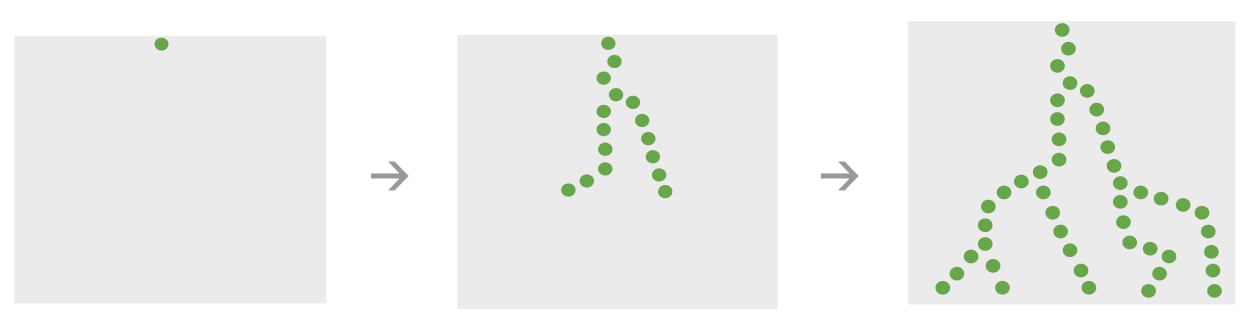
罚分像生长的树木一样向上流经知识图。

部分包含

FIRe 还自然地处理部分包含的情况，在这种情况下，只有一个较简单主题的某些部分在一个高级主题中被隐式练习。这在更高等的数学中更常见。

例如，在微积分中，高级积分技巧如分部积分要求你计算各种数学函数的积分，如多项式、指数函数和三角函数。但其中一些函数可能只出现在分部积分问题的一部分中。所以，如果你完成了一次分部积分的重复练习，你应该只获得对每个部分包含主题的一部分重复练习。

下图中，我们用数字权重标注主题间的包含关系，表示学习高级主题时涉及各个基础主题的程度。你可以将每个权重理解为：从高级主题中随机选取一个问题时，它包含某个基础主题内容的概率。

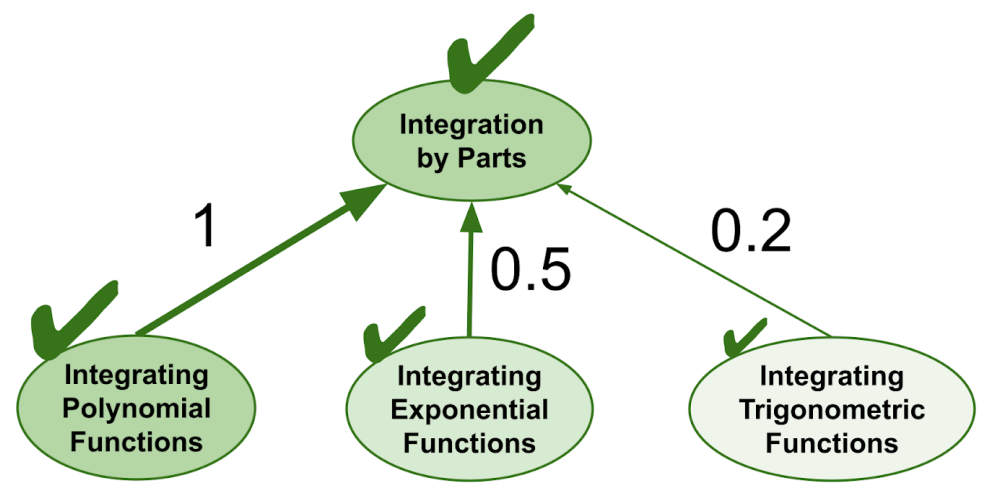
FIRe 通过这种部分包含，将重复流延伸到多个层级。最终结果是：

1. 重复练习沿着完全包含关系构成的「主干」畅通无阻地传递，

2. 同时沿着从主干分支出去的部分包含关系逐渐衰减。

手动设置包含权重

由于包含权重需要手动设置，为知识图谱中每对主题都设置明确的权重是不切实际的。我们的系统包含数千个主题，如果列出所有可能的主题对，权重矩阵将包含数千万个条目。那么，我们该如何设置这些庞大的权重数据呢？

事实上，我们并不需要明确设置矩阵中的每一个权重。只需要为满足以下条件的主题对设置权重即可：

1. 权重有一个非平凡的值，

2. 无法通过重复流推断出权重，

3. 两个主题在前置知识图中的距离较近。

并且我们假定，除了在重复流中隐式计算得出的权重外，其他所有权重均为零。这一假设基于以下理由：

1. 权重的大小反映了隐式重复所产生的学习效果。为了使隐式重复能够有效减少显式复习的需求，它必须与足够显著的学习效果相关联。

2. 如果重复流能够推断出某个权重，那么手动设置该权重通常不会改变结果（除非手动设置是为了纠正重复流可能错误推断的值）。

3. 如果两个主题在前置知识图中相距较远，即使它们之间存在完全包含关系，其权重对减少复习需求的影响也不会太大。这是因为当学生学习到更高级的主题时，他们已经对较基础的主题进行了大部分必要的显式复习。

值得注意的是，满足上述条件的权重通常分布在直接相关和关键的前置知识连接上，而这些连接的数量与主题总数呈线性关系。这一特点使得手动设置包含权重变得可行：只需为每个直接或关键的先决条件分配一个权重即可。

值得注意的是，在知识图谱中，即使某些主题之间的直接关联或关键前置知识的关联强度低至零，也是常见现象。这种情况通常出现在学习某个主题时，学生只需对其前置知识有概念性的理解，而不必精通到能够独立解决相关问题的程度。

因材施教，适应学生个体差异和主题特性

学习能力的个体差异是一个广为人知的事实。研究表明，学生之间在学习速度和记忆保持能力上存在显著差异：有些学生学习快、记忆久，而另一些则学习慢、遗忘快（例如，Kyllonen & Tirre, 1988; Zerr et al., 2018; McDermott & Zerr, 2019）。同样，不同主题的学习难度也各不相同：简单的主题往往学习速度快、记忆持久，而困难的主题则需要更长的学习时间，且更容易被遗忘。

因此，每个学生在每个主题上的学习速度都是由学生个人能力和主题难度这两个因素共同决定的。这两个因素是相互影响的：学生的高能力会加快整体学习进度，而主题的高难度则会减缓学习速度。从这个角度来看，我们可以将学生在特定主题上的学习速度化为以下两个因素的比率：

1. 学生能力带来的学习加速

2. 主题难度导致的学习减速

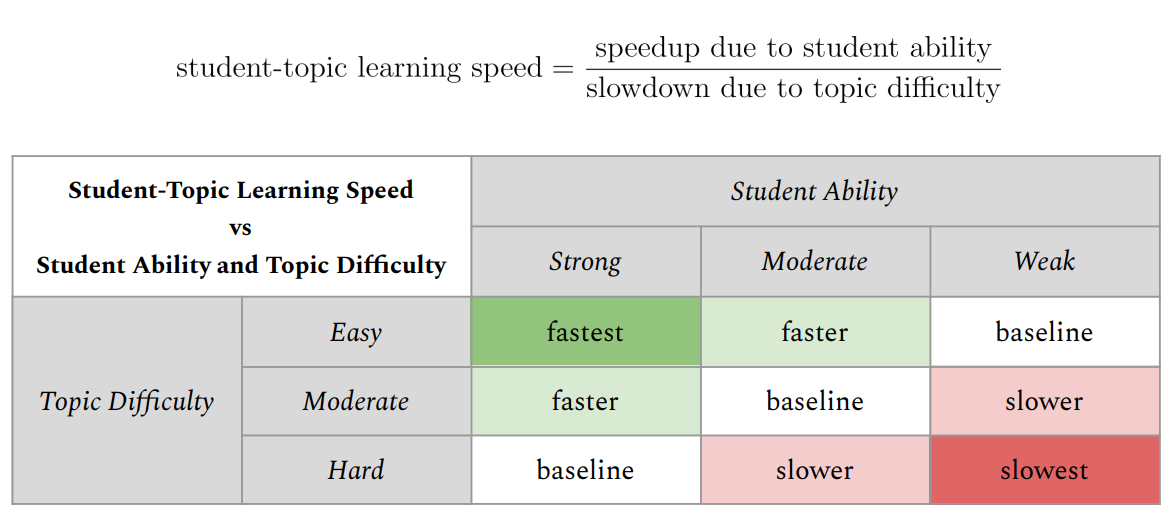
「学生-主题学习速度」这一指标用于调节间隔复习过程的进度。

• 举个例子，假设一个学生在某个主题上的学习速度是标准速度的 2 倍，那么他在这个主题上完成的一次复习就会被系统认为相当于完成了两次标准的间隔重复。

• 同样的道理，如果一个学生在某个主题上的学习速度是标准速度的 0.5 倍，那么他在这个主题上完成的一次复习就只会被系统视为完成了半次标准的间隔重复。

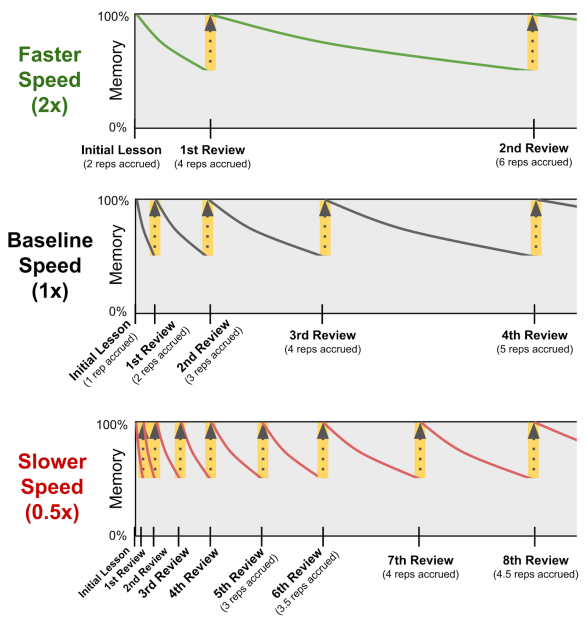
在部分隐式重复算法中，也会考虑「学生-主题学习速度」这一因素。学习能力较弱的学生通常难以在复杂主题上获得隐式重复的学习效果——他们更难理解「我之前学过的内容是我现在学习内容的一个特例（或组成部分）」这种关系。

因此，当需要放慢某个主题的间隔重复进度时（即当该学生在这个主题上的学习速度低于标准水平时)，最佳策略是取消所有即将到来的隐式重复得分，转而强制进行显式复习。换句话说，这个主题将不再接收原本应该从更高级主题「涓滴」的隐式重复得分。

根据学生在特定主题上的学习速度来决定是否需要强制进行显式复习是合理的。这是因为当某个主题的间隔重复过程变慢时，通常表明该主题对学生而言相对较难掌握。

此外，我们需要认识到，虽然诸多因素可能影响学生的学习速度，如天资、遗忘速率、兴趣或动机水平，以及学习时的疲劳程度或注意力分散等，但这些因素的重要性最终取决于它们对学生实际表现的影响。因此，每个学生的个人学习曲线可以仅根据其观察到的实际表现进行适当调整。

间隔重复模型的宏观结构

从宏观角度看，我的间隔重复模型结构可以概括如下：

$$\begin{align*} repNum &\to \max \left( 0, \phantom{,} repNum + speed \cdot decay^{, failed} \cdot netWork \right) \ memory &\to \max \left( 0, \phantom{,} memory + netWork \right) (0.5)^{ , days , / , interval} \end{align*}$$

• repNum：学生在特定主题上成功完成的间隔重复轮数。

  在以下定义中，「重复」指的是在适当时间进行的成功复习。

• days：自上次重复以来经过的天数。

• • interval：第 repNum 次重复和第 repNum+1 次重复之间的理想间隔天数。
• • memory（记忆值）：表示学生在距离上次重复一段时间后的记忆保留率期望。记忆值会随时间逐渐衰退，当记忆值降至某个阈值时，就需要进行下一次重复。另外，如果重复的时间过早（记忆值仍然较高），系统会相应降低该次重复的权重。

• speed（学习速度）：根据学生在特定主题上的表现来衡量其学习速度。这个参数决定了学生在间隔重复学习过程中进步或退步的快慢。

• failed（失败标记）：重复失败记为 1，通过则为 0。

• • netWork（净效用）：衡量学生在一次重复中产生的实际学习效果。重复通过时，netWork 为正值；失败时为负值。

  在成功的重复中，完成质量越高，netWork 的正值就越大；在失败的重复中，表现越差，netWork 的负值就越大。

  如果重复比预期间隔提前进行（即 memory 记忆值仍然较高），netWork 的数值会相应减少。

  注意，在高级主题上的成功练习也会算做对其包含的较简单主题的隐式练习；同样，在较简单主题上的失败也会对以其为基础的更高级主题产生负面影响。

• decay（衰减值）：当学生在复习中失败时，此参数表示其在间隔重复学习过程中后退速度与前进速度的比值。

  decay 衰减值是一个从 1 开始的正数，它随着重复的时间远远超过理想间隔而增大，即随着记忆严重衰退而增加。

  引入衰减值的目的是为了模拟严重的知识衰退现象，例如广为人知的「暑假滑坡」。在这种情况下，上学年末期学习的内容可能在暑假期间被严重遗忘，以至于在新学年开始时需要更频繁地复习，甚至需要完全重新学习。

针对后续问题的一些回应澄清

在这篇文章于 2024 年 7 月在 HackerNews 上引起关注后，我收到了一些很好的后续问题。以下是我想要说明的关于上述方法的一些要点。如果您还有任何这里未解答的问题，欢迎联系我。

学习者首先通过精通学习的方式接触新主题，也就是说，在他们已经了解并掌握了前置主题之前，不会学习新主题。只有在复习阶段，我们才会进行所有涉及隐式「消除」重复的操作。

**学生并不是简单地记忆答案。**每次的问题都是不同的，虽然测试相同的概念或过程，但不允许学生简单地记忆答案。

这种学习策略是否仅适用于数学，还是也能应用于其他领域的概念学习？

这种策略之所以强大，在于它充分利用了数学知识结构的层次性和高度包含性。任何具有密集包含关系的知识领域都应该能够采用这种策略。然而，如果某个知识领域缺乏紧密的包含关系，那么你能够通过隐式方式「消除」的复习量就会大大受限。

如果学生在学习新主题时，发现自己忘记了某个必要的前置知识，会怎么样？

对此，我们有理论和实践两方面的保障措施。为了便于解释，让我们假设主题 A 是主题 B 的前置知识。

理论保障

如果你有可能在近期忘记 A，那么你现在就会收到一个针对 A 的重复提醒。这意味着你需要立即复习 A（如果可能的话，通过学习更高级的主题来「隐式消除」这个复习需求；如果不可能，我们就会给你一个针对 A 本身的显式复习）。

总的来说，如果某个重复到期，我们不会一直等待出现「隐式消除」的机会，以免你在等待过程中遗忘。我们会直接判断「看来现在无法隐式消除这个复习需求」，然后给你一个显式复习。

实际保障

假设由于某些原因，复习的时间安排略有偏差，导致学生在学习 B 内容时，对先前学过的 A 内容遗忘得比预期更多。即便如此，他们也不会完全忘记 A，而且可以相对轻松地重新温习。通常，这种温习机会就蕴含在 B 的内容中。举例来说，当你学习解决 ax+b=cx+d 形式的方程时，讲解过程中必然会全面回顾如何解 ax+b=c 这类方程。

即便在其他情况下，这种回顾可能不那么详尽，如果你对 A 内容记忆模糊到难以理解 B 的解释，你随时可以回顾学习 A 时的内容进行复习：「嗯，B 中的这部分内容看着眼熟，但它涉及到A，我忘了 A 的某些步骤…好，让我看看 A 的课程…啊对了，我想起来了，就是这么做的。现在回到 B。」而后，在解决 B 中的问题时，你对 A 的刷新记忆会得到进一步巩固。

在最糟糕的情况下，如果学生彻底忘记了 A，以至于无法通过查看参考资料来复习，我们还设有一套补救机制，可以为他们显式提供针对 A 内容的额外练习。在 B 的课程中，我们会追踪前置知识的应用情况，所以如果学生在 B 的学习中「遇到瓶颈」（即连续两次未能通过课程，且第二次没有任何进步），我们就会针对学生卡住的前置知识启动补救性学习任务。

但是，我们是否可以设想，即使子概念和父概念形成了层级关系，回答子概念也不一定能激活父概念？

这正是我们需要明确区分「前置知识」和「包含关系」的关键所在。我承认，我本应在文章中更详细地解释这一点。的确，前置知识并不总是会被自动激活。如果你在前置知识图上应用 FIRe 方法，并将前置知识等同于包含关系，那么你会得到大量错误的重复得分的涓滴。

事实上，我们在早期就遇到了这个问题。解决方案是我必须运用自己的领域专业知识，手动构建一个「包含图」。这项工作量巨大，与手动构建前置知识图同样繁琐。你可以将前置知识图理解为一个「前向」图，它展示了你接下来可以学习的内容；而包含图则是一个「后向」图，它显示了你在学习后续主题时，如何将获得的知识回溯应用，从而为早期学习的主题赋予得分。

手动构建包含图确实是一项令人头疼的工作。我花费了大量时间仔细审视每个主题，不断问自己这样一个问题：「如果一个学生能够解决『后续』主题的问题，我们是否可以合理地认定他们已经真正掌握了前置主题？」诚然，为了使学习过程顺利进行，学生需要预先学习先前置知识，这一点是不言而喻的。但是，这个前置知识是否真的代表了我们确信学生正在练习的核心技能呢？」研究结果表明，在许多情况下答案是「否定的」——但也有相当多的情况是肯定的。而且，这些肯定的情况足以对学习效率产生巨大影响，前提是我们能够充分利用它们。

每当我们推出新主题或调整现有主题时，我都需要更新包含图。要完成这项工作，必须对图中所呈现的知识领域有深入的专业理解。（通常情况下，我们的课程总监负责管理前置知识图，而我负责管理包含图。）

这种方法有任何学术研究成果吗？对间隔重复系统（SRS）的这种改进是否有效？它对哪类学生有帮助？如果确实有效果，效果有多显著？

这种方法的核心理念是使间隔重复在数学等领域变得切实可行。如果没有这种方法，间隔重复将难以实施，因为学习者很快就会被海量复习任务压得喘不过气来，导致无法在学习新知识方面取得任何进展。

更为重要的是，间隔重复不仅使这种学习方式切实可行，还在确保充分复习的前提下将复习量降到最低，从而让你能够突飞猛进。

目前，我们 Math Academy 尚未发布正式的学术研究成果。然而，如果你想要一些更具体的学习效率证据，可以上网查阅更多关于我们在 Pasadena 开展的原创校内项目的信息。在这个项目中，我们的六年级学生从预代数起步，到八年级结束时就能掌握全部高中数学课程（包括代数1、几何、代数 II 和预微积分）。不仅如此，他们还在八年级学习 AP 微积分 BC 课程并参加相应的 AP 考试。

在采用传统人工教学时，学生们的 AP 考试成绩就已经相当不错了。但自从我们开始使用自动化系统（其中包含了前面提到的间隔重复系统）后，AP 微积分 BC 考试的成绩更是显著提升。绝大多数学生都顺利通过了考试，而且在通过的学生中，大部分都获得了满分（5 分制中的 5 分）。值得一提的是，那一年还有四名与我们 Pasadena 学校项目无关的学生，完全脱离课堂环境，仅依靠我们的系统学习 AP 微积分 BC。结果除了一人，其他全都在 AP 考试中拿到了满分 5 分（剩下那位也取得了 4 分的优异成绩）。

一些看似不可能的事情竟然开始发生了。例如，有些学习动力极强的六年级学生，从预代数课程中途开始学习，却在短短一个学年内就完成了通常需要整个高中阶段才能学完的数学课程（包括代数 I、几何、代数 II 和预微积分），甚至开始学习 AP 微积分 BC。有趣的是，当 Math Academy 的创始人 Jason 和 Sandy 第一次看到一个六年级学生接到 AP 微积分 BC 的作业时，Jason 惊呼道：「这是怎么回事？我们的模型出问题了吗？为什么这个孩子会接到微积分的作业？他去年秋天才刚开始学预代数啊，这完全说不通。」但经我调查后发现，这竟然是真的——这个孩子确实在一个学年内就完成了全部高中数学课程。

如果你对此感兴趣，可以查看以下链接：mathacademy.us/press、相关 Reddit 讨论、我在 X/Twitter 上分享的故事，以及该故事的后续。

再次声明，我明白这些并非正式的学术研究。但目前我们正全身心投入创业，产品开发上有太多事情需要处理，以至于我们根本没有时间进行学术研究，连整夜安眠都成了奢望。

如果不做这些改进来减少复习量，间隔重复真的就无法有效实施吗？

我一直在使用 Anki 这款软件来学习和记忆大量数学知识。虽然它并非完美无缺，我也很希望能有一个有向无环图式的学习系统来更好地组织知识，但根据我的经验，基础主题一旦被充分理解，往往会被系统自动推迟很长时间才进行复习。这意味着我可能一年都不会被要求回顾某个基础主题或问题。这种间隔重复的机制似乎有效地避免了重复卡片过多导致的学习负担，让学习更加高效。

然而，有时当我遇到一个较为深奥的知识点时，却发现自己已经遗忘了相关的基础知识，这种情况会让人感到沮丧。因为我不得不直接应对这个高级主题，而无法从最基础的概念（即这个主题的「祖先」知识点）开始，循序渐进地复习一系列相关的前置知识。

诚然，只要我能每天坚持使用 Anki，即使只花 10 到 20 分钟，我就不会忘记任何基础知识。这凸显了持续学习的重要性。然而，如果我中断使用 2 到 3 个月，再重新回到我的卡片组，我可能就会面临前面提到的问题，有时甚至不得不手动搜索相关的基础知识点来进行复习。

你提出的这些观点确实很有道理。我认为，间隔重复的可行性，主要取决于我们如何定义「重复」这个概念。如果你把对一个主题进行一次简单快速的练习就视为一次重复，而且你学习的主题数量不多，学习进度也不会太快，那么这种方法确实如你所说是可行的。

然而，值得注意的是，Math Academy 是基于一个不同的理念设计的：

• 我们的课程体系涵盖了海量的学习主题（以我们的 AP 微积分 BC 课程为例，就包含了 300 多个主题——而这仅仅是一门课程而已；如果学生在完成第一门课程后继续在我们的平台上学习更多课程，他们很容易就能积累起需要维持的数千个主题）

• 每次复习都包含多个关于该主题的问题（初次学习时，一个课程任务大约包含 10 个问题，之后的复习任务则通常包含 3-5 个复习问题）

• 学生平均每 20 分钟左右就能掌握一个新主题（以我们的 AP 微积分 BC 课程为例，整个课程预计需要约 6000 分钟，这已经包括了复习、测验等在内的所有时间。具体计算为：6000 分钟 ÷ 300 个主题 = 每个主题平均 20 分钟）

让我们用一些简单的估算来说明我们系统的运作方式：假设你每天学习 3 个新主题（相当于一小时的学习时间），每次复习大约需要回答 4 个问题。那么，根据粗略估计，你很快就会达到这样一个学习状态：

• 12 个关于昨天所学内容的复习问题，

• 再加上 12 个关于上周首次复习内容的复习问题，

• 再加上 12 个关于两周前第二次复习内容的复习问题，再加上 12 个关于一个月前第三次复习内容的复习问题，

• 再加上 12 个关于几个月前第四次复习内容的复习问题，

• ...

这意味着每天需要复习 60 个问题，远远超出了你在每次一小时学习中能够全部用于复习的时间，导致学习新知识的进度完全停滞。

因此，至少在我们的教学场景中，原始的间隔重复并不可行——除非我们采取措施大幅减少复习量（比如使用部分隐式重复和重复压缩），否则学生将会被海量的复习任务彻底淹没。

当然，我理解你提出的观点，即如果中断学习 2-3 个月后重新开始，确实需要一些复习。Math Academy 的学生如果休息一段时间后重新学习，也会遇到类似的情况。但我们解决这个问题的方法是建议他们重新进行一次诊断性测试，以更新他们的知识状况。本质上，这个过程就是将他们的「知识边界」适当回调，使他们能够从一个合适的起点重新开始，然后顺利地采用我们的标准学习方法继续学习。

（根据我的经验，这正是教师在暑假结束后应该做的——你意识到学生已经遗忘了大量知识，所以你让他们参加一个新学年初的知识评估，然后基于评估结果开展教学。）

参考文献

Kyllonen, P. C., & Tirre, W. C. (1988). Individual differences in associative learning and forgetting. Intelligence, 12(4), 393-421.

McDermott, K. B., & Zerr, C. L. (2019). Individual differences in learning efficiency. Current Directions in Psychological Science, 28(6), 607-613.

Zerr, C. L., Berg, J. J., Nelson, S. M., Fishell, A. K., Savalia, N. K., & McDermott, K. B. (2018). Learning efficiency: Identifying individual differences in learning rate and retention in healthy adults. Psychological science, 29(9), 1436-1450.

本文是 The Math Academy Way（2023 年 10 月草稿）的一部分。 引用格式： Skycak, J., advised by Roberts, J. (2023). Optimized, Individualized Spaced Repetition in Hierarchical Knowledge Structures. In The Math Academy Way (Working Draft, Oct 2023). https://justinmath.com/individualized-spaced-repetition-in-hierarchical-knowledge-structures/